[Algorithm]알고리듬 분석

📚알고리듬 분석

📄정확성 분석

정확한 알고리듬은 유효한 입력에 대해 유한 시간 내에 정확한 결과를 생성해야 한다.

정확성 분석은 수학적 기법을 사용한 이론적인 증명 과정이라고 할 수 있다.

📄효율성 분석

알고리듬의 효율성 분석은 알고리듬을 수행하는데 얼마나 많은 컴퓨터 자원이 필요한지 평가하는 것이다.

• 공간 복잡도: 알고리듬 수행에 필요한 총 메모리 양(정적 공간 + 동적 공간).

• 시간 복잡도: 알고리듬의 수행시간. 실행 부터 완료까지 걸리는 시간.

알고리듬의 실제 수행시간을 측정하는 방법은 실행 환경에 종속적이다. 컴퓨터 속도, 프로그래밍 언어, 컴파일러 효율성 등에 따라 수행시간이 달리질 수 있기 때문에 일반성이 결여된 방법으로서 알고리듬을 분석하는데 적합하지 못한 방법이다.

종속적인 문제를 해결하고 객관적인 알고리듬의 수행시간을 측정하기 위해 각 문장(연산)이 수행되는 횟수를 계산하고 이 횟수들을 모두 더한다.

하지만 위 방법도 입력 크기, 입력 데이터의 상태에 따라 알고리듬의 수행시간이 달라진다는 문제점이 있다.

• 입력 크기에 따른 알고리듬 수행시간

입력 크기 n이 커질수록 수행시간도 증가하므로 단순히 단위 연산이 수행되는 개수의 합으로 표현하는 것은 부적절하다. 따라서 수행시간은 입력 크기 n의 함수로 표현하는 것이 바람직 하다.

• 입력 데이터의 상태에 따른 알고리듬 수행시간

모든 입력 상태에 대해 각각의 수행시간을 계산하고 이들의 평균을 내는 것이 이상적이지만 모든 입력 상태와 각각의 수행시간을 알기 어렵다는 문제가 있다.

최선 수행시간은 모든 입력 상태의 수행시간 중 가장 빠른 시간을 의미하는데 이런 접근 방법 역시 입력 데이터의 상태가 항상 최적이라고 가정할 수 없기 때문에 적합한 알고리듬 수행시간을 구하는 방법이라고 볼 수 없다.

따라서 일반적으로 평균, 최선 수행시간이 아닌 최악 수행시간을 알고리듬의 시간 복잡도의 척도로 많이 사용한다. 최악 수행시간은 모든 입력 상태의 수행시간 중 가장 느린 시간을 의미한다.

최악의 수행시간은 어떤 입력이 들어와도 이를 초과하는 수행시간은 걸리지 않는다는 보장이 있어서 알고리듬 간의 성능을 비교할 때 유용하다.

위의 내용을 요약하면 일반적으로 알고리듬의 시간 복잡도는 입력 크기 n의 함수와 최악 수행시간으로 표현한다는 것이다.

#include<stdio.h>

// T(n)을 입력 크기 n에 대한 알고리듬 수행시간이라고 하자.
// SumAverage 알고리듬의 수행시간은 T(n) = 3n + 5 이다.
void SumAverage(int arr[], int n)
{
	int sum = 0;	// 1
	int i = 0;	// 1

	while (i < n)	// n + 1
	{
		sum += arr[i];	// n
		++i;		// n
	}

	int average = sum / n;	// 1

	printf("sum: %d, average: %d", sum, average);	// 1
}

int main()
{
	int arr[] = { 1, 2, 3, 4, 5 };
	int arrSize = sizeof(arr) / sizeof(int);

	SumAverage(arr, arrSize);
}

📄점근성능

점근성능이란 입력 크기 n이 무한히 커짐에 따라 결정되는 성능을 말한다. 다항식의 수행시간에서 입력 크기 n이 무한히 커짐에 따라 함수값(수행시간)이 어떻게 증가하는지 추세를 살펴보면 최고 차수를 가진 항에 의해 가장 큰 영향을 받는 것을 알 수 있다.

점근성능을 결정하는 것은 입력 크기가 충분히 커짐에 따라 함수값에 가장 큰 영향을 미치는 차수를 찾는 것이다. 따라서 알고리듬의 수행시간을 점근성능으로 표현한다는 것은 수행시간의 다항식 함수에서 최고차항만을 계수 없이 찾아 단순화시킨 형태로 성능을 표현하는 것이다.

알고리듬의 점근성능은 수행시간의 정확한 값이 아닌 어림값으로서 정확한 수행시간은 알 수 없지만 증가 추세를 파악하거나 알고리듬 간의 우열을 따질 때 유용하다는 장점이 있다.

• O-표기(점근적 상한) -> 최악의 수행시간

어떤 양의 상수 c와 n₀이 존재하여 모든 n >= n₀에 대하여
f(n) <= c·g(n)이면 f(n) = O(g(n))이다.

• Ω-표기(점근적 하한) -> 최선의 수행시간

어떤 양의 상수 c와 n₀이 존재하여 모든 n >= n₀에 대하여
f(n) >= c·g(n)이면 f(n) = Ω(g(n))이다.

• Θ-표기(점근적 상하한) -> 정밀한 성능 측정

어떤 양의 상수 c와 n₀이 존재하여 모든 n >= n₀에 대하여
c₁·g(n) <= f(n) <= c₂·g(n)이면
f(n)=O(g(n)) = Ω(g(n))이면 f(n) = Θ(g(n))이다.

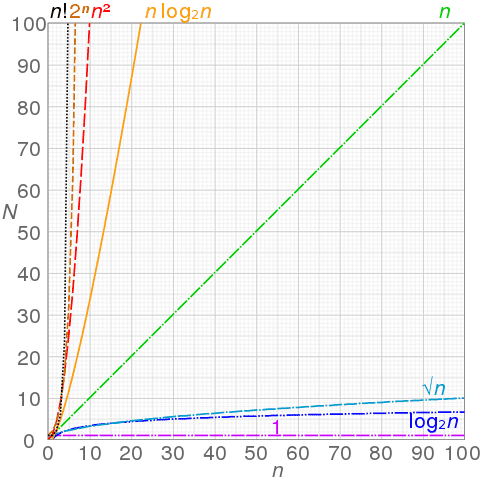
알고리듬의 시간 복잡도는 일반적으로 O-표기법을 사용하여 나타낸다. 자주 사용하는 여러 함수의 크기 관계를 비교하면 아래와 같다. 왼쪽에서 오른쪽으로 갈수록 시간이 오래 걸리고 효율성이 떨어진다.

\[O(1) < O(\log n) < O(n \log n) < O(n^2) < O(n^3) < O(2^n)\]

알고리듬의 시간 복잡도를 구하는 실용적인 접근 방법으로는 알고리듬의 모든 문장이 아닌 루프의 반복 횟수만을 조사여 최고 차수를 시간 복잡도로 취하는 방법이 있다.

위의 SumAverage 알고리듬의 수행시간 T(n) = 3n + 5를 점근성능으로 간단하게 표현하면 O(n)으로 표현할 수 있다.

📄순환 알고리듬

순환 알고리듬은 알고리듬의 수행 과정에서 자기 자신의 알고리듬을 다시 수행하는 형태이다.

int BinarySearch(int left, int right, int* array, int key)
{
	if (left > right)
	{
		return -1;
	}

	int mid = (left + right) / 2;

	if (array[mid] == key)
	{
		return mid;
	}
	else if (key < array[mid])
	{
		BinarySearch(left, mid - 1, array, key);
	}
	else
	{
		BinarySearch(mid + 1, right, array, key);
	}
}

순환 알고리듬의 성능은 루프가 있는 알고리듬 같이 몇 번 수행되는지 알기 어렵기 때문에 일반적으로 점화식의 형태로 나타낸다.

📄점화식

점화식이란 어떤 하나의 값이 자기 자신을 포함하는 어떤 수식으로 표현되는 식을 말한다.

위의 BinarySearch()를 점화식으로 나타내면 T(n) = T(n/2) + O(1), T(1) = c₁이 된다.

3 ~ 13줄은 O(1)이고, 14 ~ 21줄은 둘 중 하나만 실행되기 때문에 T(n/2)가 된다.

T(n) = T(n/2) + O(1), T(1) = c₁ 점화식의 폐쇄형을 구하면 Θ(log₂n)이 된다.

기본 점화식과 폐쇄형은 아래와 같다.

📄효율적인 알고리듬

입력 크기가 커질수록 알고리듬 수행시간의 차이가 확연하게 나기 때문에 효율적인 알고리듬의 설계와 선택이 중요하다.