[Circuits]수치 데이터

📚진법

📄수와 숫자

수는 숫자라는 기호로 나타냅니다.
수는 하나의 개념이고 숫자는 사람들이 의사소통을 위해 정한 기호인 것 입니다.

📄진법

진법은 숫자의 위치에 따라 가중치를 부여하는 방법입니다.
가중치는 기수의 승수를 이용합니다. 기수는 2 이상의 양의 정수이고 기수가 r인 경우 r진법이라고 합니다. r진법은 r개의 숫자로 수를 표현하고 이렇게 표현된 수를 r진수라고 합니다.
예를 들면, 10진법은 10개의 숫자(0 ~ 9)로 수를 표현하고 2진법은 2개의 숫자 0, 1로 수를 표현합니다.

12.1₁₀ = 1 X 10¹ + 2 X 10⁰ + 1 X 10^-1
101.01₂ = 1 X 2² + 0 X 2¹ + 1 X 2⁰ + 0 X 2^-1 + 1 X 2^-2

📄진수변환

1. r진수의 10진수 변환
   다음 식들을 보면 간단하게 r진수를 10진수로 변환할 수 있을 것 입니다.
   
   11.01₂ = 1 X 2¹ + 1 X 2⁰ + 0 X 2^-1 + 1 X 2^-2
   　　　 = 2 + 1 + 0 + 0.25
   　　　 = 3.25
   
   1A.2₁₆ = 1 X 16¹ + 10 X 16⁰ + 2 X 16^-1
   　　　 = 16 + 10 + 0.125
   　　　 = 26.125
   
   

2. 10진수의 r진수 변환
   10진수 123.125를 2진수로 변환하면 정수부분 123이 몫이 0이 될때까지 2로 계속 나눠주면 됩니다. 소수부분 변환은 0.125가 1이 될때까지 2를 계속 곱해주면 됩니다. r진수 변환은 앞에서 예를 들었던 2대신 r로 계속 나누거나 곱해주면 됩니다.
   
   　　정수부분 변환　　　　　　　　소수부분 변환
   　　　
   
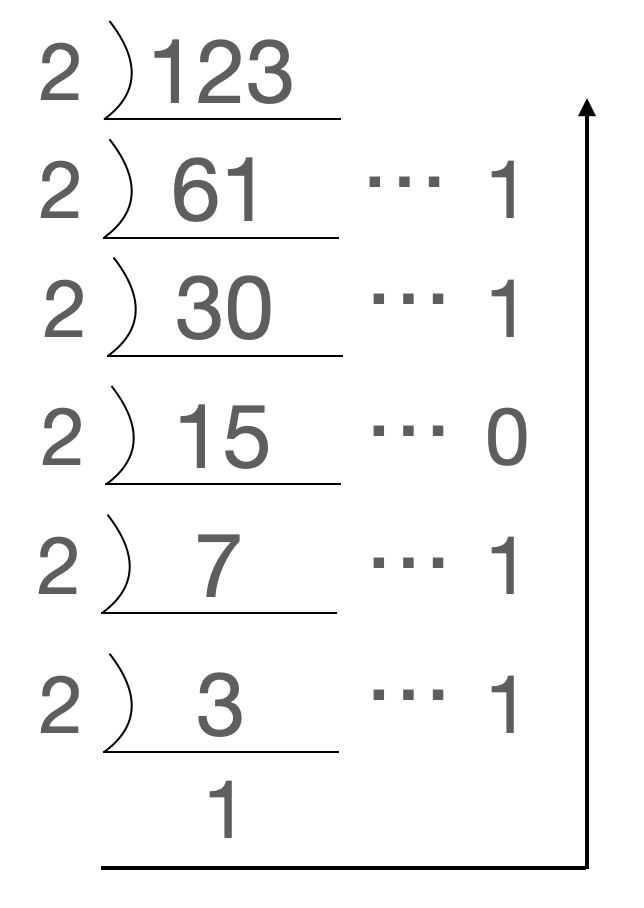
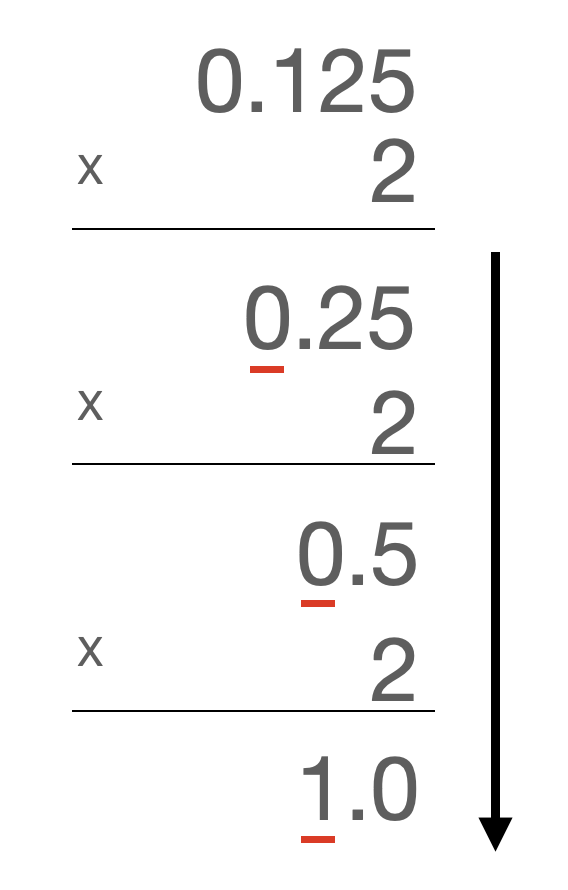
   123.125₁₀ = 11011.001₂이 됩니다.
   
   간혹 10진수 0.3 같이 2진수로 변환할 때 소수부분이 0이 되지 않고 2를 곱할 때 무한히 계산되는 경우가 있습니다. 이런 경우 필요한 만큼 잘라서 사용하면 됩니다.
   
   

3. 2진수와 2ⁿ진수의 상호 변환
   2진수를 구성하는 각 자릿수는 비트라고 합니다. 2개의 비트는 00, 01, 10, 11을 표현할 수 있고 이는 모두 4(2²)개입니다. 일반적으로 n개의 비트로는 2ⁿ개의 수를 표현할 수 있습니다.
   2진수를 4진수, 8진수, 16진수 등으로 변환하고 그 역의 변환 방법에 대해 알아봅시다.
   
   2진수의 비트를 소수점을 중심으로 2개씩 묶으면 00, 01, 10, 11 조합을 얻을 수 있습니다. 이는 각각 한 자리의 4진수 0, 1, 2, 3에 대응됩니다. 8진수는 2진수를 3비트씩 묶으면 되고 16진수는 2진수를 4비트씩 묶어서 변환할 수 있습니다.
   
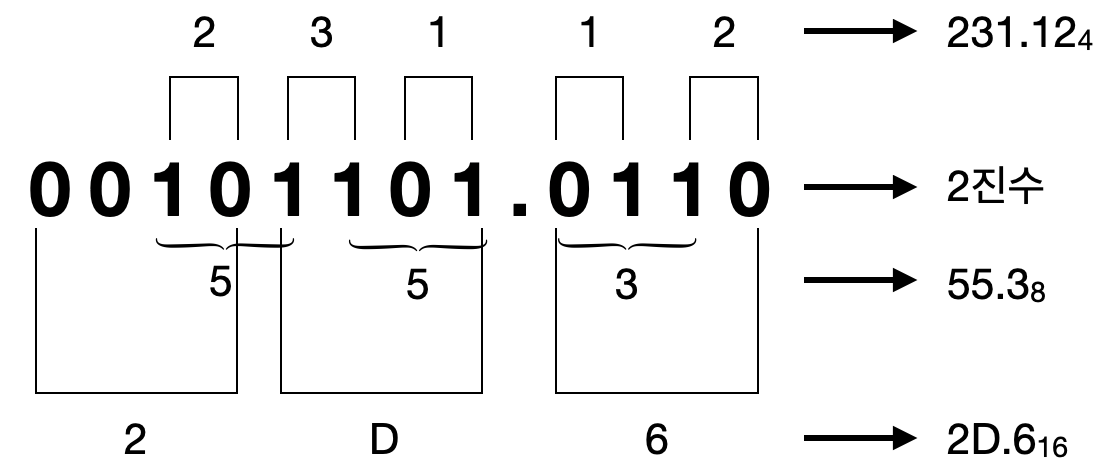
   2진수 비트들을 n비트씩 묶을 때 부족한 비트 수만큼 0이 있다고 가정해야합니다.
   2ⁿ진수를 2진수로 변환할 때는 2ⁿ의 각 자리 수에 대응하는 n비트의 2진수로 모두 바꾸면 됩니다. 예를 들어 16진수 2D.6₁₆을 2진수로 변환하면 2, D, 6을 2진수로 각각 변화하면 됩니다.
   
   

4. 기타변환
   r진수를 s진수로 변환하는 경우 먼저 r진수를 10진수로 바꾼 다음 10진수를 s진수로 변환합니다.
   예를 들어 5진수를 8진수로 변환한다고 했을 때 5진수를 10진수로 변환하고 바꾼 10진수를 8진수로 변환하면 됩니다.

📄산술연산

r진수에 대한 산술연산은 10진수의 산술연산과 같습니다. r진수는 r개의 숫자만 사용할 수 있다는 것만 다릅니다.

• 2진수 가산(덧셈)
  101₂ + 100₂ = 1001₂

• 2진수 제산(뺄셈)
  1101₂ - 111₂ = 110₂

• 2진수 승산(곱셈)
  110₂ * 11₂ = 10010₂

• 2진수 제산(나눗셈)
  2진수의 나눗셈은 나누어지는 수(피제수)에서 나누는 수(제수)를 계속 빼서 나누어지는 수가 나누는 수보다 최초로 작아지거나 0이 될 때, 그때까지 뺀 횟수가 몫이 되고 빼고 남은 값이 나머지가 됩니다.
  
  110101₂ / 110₂ = 1000₂, 나머지 101₂

2진수가 아닌 r진수들의 산술연산은 10진수로 변환하여 연산을 진행해주는 것이 편합니다.

📚보수

보수를 이용하여 컴퓨터에서의 감산이 가산만으로도 가능하다는 것을 설명할 수 있습니다. r진수 N은 r의 보수와 r-1의 보수 두가지 보수가 있습니다.

📄보수의 개념

• r의 보수
  

\[N에\;대한\;r의\;보수 = \begin{cases}r^n-N,&N ≠ 0 \\ 0,&N = 0 \end{cases}\]

• r-1의 보수
  

정수부분이 n개의 자리로 구성되고 소수점 아래가 m개의 자리로 구성된 r진수 N에 대한 r-1의 보수에 대한 식입니다.

\[N에\;대한\;(r-1)의\;보수 = r^n - r^m - N\]

r의 보수와 r-1의 보수의 관계는 아래와 같습니다.

\[r의\;보수 = (r-1)의\;보수 + 가장\;낮은\;자리의\;1\]

📄보수를 이용한 감산

감수를 부호를 포함하여 r의 보수를 한 다음 피감수에 가산합니다.

\[\pm A - (\pm B) = \pm A + (\mp B)\]

📚부호 있는 2진수

📄부호 있는 절대치 표현

부호 있는 절대치 표현방법은 수의 크기와 부호를 나타내는 비트로 구성하여 표현합니다.

실생활에서 우리는 음수와 양수를 구분하기 위해 숫자 앞에 부호를 씁니다. 비트로도 음의 정수를 표현하기 위해 부호와 같은 역할을 하는 비트를 정했습니다. 가장 왼쪽에 위치한 비트(MSB)를 부호로 약속하고 이 부호 비트가 1이면 음수, 0이면 양수로 표현합니다.

예를 들어 4비트 크기의 값이 있을 때 MSB를 부호 비트로 정하고 나머지 3비트를 사용하여 수를 표현할 수 있습니다. 따라서 -7부터 7까지 표현할 수 있습니다. 쉽게 말하면 가장 왼쪽의 비트가 부호를 결정하는 비트가 되는 것 입니다.

부호비트를 사용하여 간단하게 2진수에 부호를 표현할 수 있지만 이 표현 방법은 0을 표현하는 방법이 두 개가 된다는 문제가 있습니다.

　　　　양수　　　　　　　　　음수

부호	22	21	20	십진수		부호	22	21	20	십진수
0	1	1	1	+7		1	0	0	0	-0
0	1	1	0	+6		1	0	0	1	-1
0	1	0	1	+5		1	0	1	0	-2
0	1	0	0	+4		1	0	1	1	-3
0	0	1	1	+3		1	1	0	0	-4
0	0	1	0	+2		1	1	0	1	-5
0	0	0	1	+1		1	1	1	0	-6
0	0	0	0	+0		1	1	1	1	-7

💡MSB와 LSB
MSB(Most Significant Bit, 최상위 비트)는 최고값을 갖는 비트 위치입니다. msb는 가장 큰 숫자를 왼쪽에 기록하는 자리 표기법의 규정 때문에 가끔 “left-most bit”를 뜻하기도 합니다.

LSB(Least Significant Bit, 최하위 비트) 이진 정수에서 짝수인지 홀수인지를 결정하는 단위값이 되는 비트 위치입니다. 최하위 비트는 가장 적은 숫자를 오른쪽에 기록하는 자리 표기법의 규정 때문에 “right-most bit”라고 부르기도 합니다.

📄부호 있는 1의 보수 표현

부호 있는 1의 보수 표현방법은 양수의 경우 부호 있는 절대치 표현방법을 따르고 음수의 경우 부호를 제외한 그 수에 대한 1의 보수를 이용하여 표현합니다.

쉽게 말해 음수를 비트로 표현하는 방법 중 모든 비트를 반전시켜 뒤집는 방법입니다. 0을 1로 1을 0으로 반전시켜 음수로 표현하는 방법이 1의 보수 표현법입니다. 1의 보수 표현법에도 부호 비트를 사용합니다. 아래 표를 보면 +1인 0001₂의 비트를 뒤집어 -1인 1110₂으로 표현된 것을 볼 수 있습니다.

하지만 이 방법도 0을 표현하는 방법이 두 개인 문제가 여전히 있습니다.

　　　　양수　　　　　　　　　음수

부호	22	21	20	십진수		부호	22	21	20	십진수
0	1	1	1	+7		1	1	1	1	-0
0	1	1	0	+6		1	1	1	0	-1
0	1	0	1	+5		1	1	0	1	-2
0	1	0	0	+4		1	1	0	0	-3
0	0	1	1	+3		1	0	1	1	-4
0	0	1	0	+2		1	0	1	0	-5
0	0	0	1	+1		1	0	0	1	-6
0	0	0	0	+0		1	0	0	0	-7

📄부호 있는 2의 보수 표현

부호 있는 2의 보수 표현방법은 양수의 경우 부호 있는 절대치 표현 방법을 따르고 음수의 경우 부호를 제외한 그 수에 대한 2의 보수를 이용하여 표현합니다.

0을 표현하는 방법이 두 개가 되는 위의 문제들을 해결하기 위해 2의 보수 표현법을 사용할 수 있습니다. 2진수의 모든 자리의 숫자를 뒤집고 1을 더하면 2의 보수를 얻을 수 있습니다. 예를 들어 +1인 0001₂을 반전시켜 1110₂에 1을 추가하면 1111₂이 -1이 되는 것입니다. 그리고 MSB에서 올림이 발생하면 버립니다.

　　　　양수　　　　　　　　　음수

부호	22	21	20	십진수		부호	22	21	20	십진수
0	1	1	1	+7		1	1	1	1	-1
0	1	1	0	+6		1	1	1	0	-2
0	1	0	1	+5		1	1	0	1	-3
0	1	0	0	+4		1	1	0	0	-4
0	0	1	1	+3		1	0	1	1	-5
0	0	1	0	+2		1	0	1	0	-6
0	0	0	1	+1		1	0	0	1	-7
0	0	0	0	+0		1	0	0	0	-8

2의 보수 표현법에서 0을 표현하는 방법은 한 가지 입니다. +0인 0000₂을 뒤집으면 1111₂이 되고 여기에 1을 더하면 MSB에 올림이 발생하는데 MSB에서 올림이 발생하면 그 값은 버린다고 했으므로 0000₂과 같아집니다.

2의 보수 표현법으로 비트 덧셈 연산을 수행하여 0을 만들어 보면 다음과 같습니다. +1인 0001₂과 -1인 1111₂을 더하면 MSB에 올림 값 1이 생겨 10000₂이 되는데 올림 값 1을 버리면 나머지 비트들은 0000₂이 되어 결과는 10진수로 0인 0000₂이 됩니다.