[DiscreteMath]함수

📚기본사항

📄함수

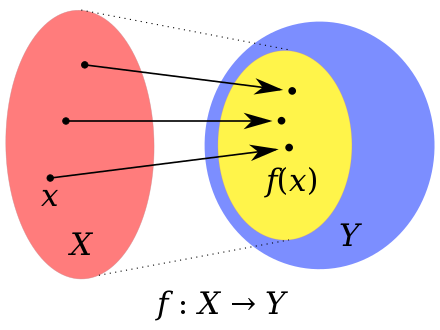
두 집합 X와 Y가 있을 때, X에서 Y로의 함수 \(f\)는 X의 모든 원소가 각각 Y의 오직 하나의 원소와 대응되는 관계입니다. 기호는 \(f : X \rightarrow Y\)로 표기합니다.

X를 함수 \(f\)의 정의역이라고 하며, Y를 함수 \(f\)의 공역이라고 합니다.

함수\(f\)에 의해 정의역의 원소 x가 공역 원소 y와 대응하는 것을 \(xfy\), \((x,y) \in f\) 또는 \(f(x) = y\)로 표기합니다.

y를 x에 대한 상이라고 하고, 함수\(f\)는 X의 원소 x를 Y의 원소 y로 사상하는 역할을 합니다.
정의역 X의 원소 x에 대한 모든 상의 집합을 치역이라고 하고 \(f(X)\)로 나타냅니다. 그리고 x를 y의 역상이라고 합니다.

https://en.wikipedia.org/wiki/Surjective_function

함수 중 이름이 붙여진 함수가 여러 개 있습니다.

• 상수함수: 정의역 값에 관계없이 항상 동일한 값이 나오는 함수
• 함등함수: 어떠한 값을 입력하더라도 그대로의 값이 나오는 함수
• 제곱함수: 함수의 출력값은 항상 입력 값의 제곱을 출력

📄함수의 상등

정의역과 공역이 같고 정의역 임의의 원소 x에 대해 \(f(x) = g(x)\)의 값이 같을 때, 두 함수 \(f\)와 \(g\)는 서로 상등하다라고 합니다. 기호로 \(f = g\)로 표기합니다.

📚전사함수, 단사함수, 역함수

📄전사함수

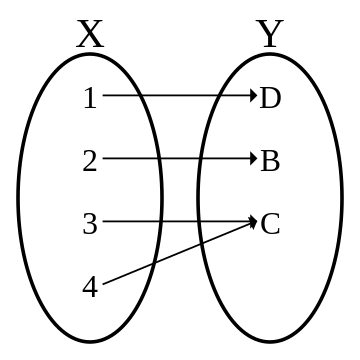
전사함수는 공역과 치역이 일치하는 함수를 말합니다. 공역 Y 임의의 원소 y에 대해 \(f(x) = y\)가 되는 x가 정의역 X에 적어도 하나 존재할 경우 함수 \(f\)를 전사함수라고 합니다.

https://en.wikipedia.org/wiki/Surjective_function

📄단사함수

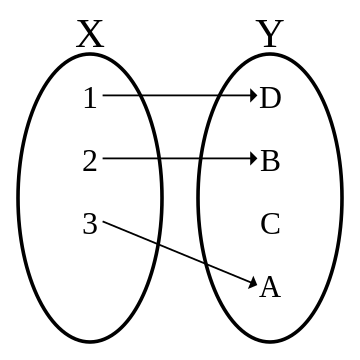
단사함수는 정의역에 있는 모든 원소가 서로 다른 상을 갖는 함수를 말합니다. 치역 임의의 원소 y에 대응하는 정의역 원소가 하나뿐일 때 함수 \(f : X \rightarrow Y\)를 단사함수라고 합니다.

https://en.wikipedia.org/wiki/Surjective_function

📄전단사함수

전사함수이면서 단사함수일 경우 전단사함수라고 합니다. 수식으로 나타내면 아래와 같습니다.

\[\begin{gather} \forall y \in Y, \;\; \exists x \in X, \;\; f(x) = y이고, \\ \forall a, \forall b \in X, \;\; f(a) = f(b)일 \; 경우 \; a = b 입니다. \end{gather}\]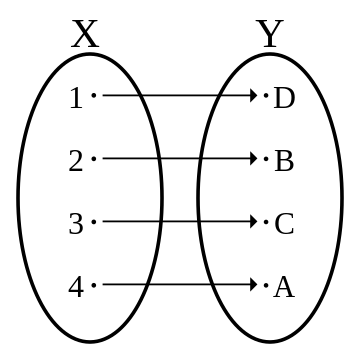

https://en.wikipedia.org/wiki/Surjective_function

📄역함수

\(f:X \rightarrow Y\)가 전단사함수일 때, \(f\)의 역관계, 함수 \(f^{-1}:Y \rightarrow X\)를 \(f\)의 역함수라고 합니다. 역관계는 함수가 수행한 일을 원래대로 되돌리는 역할을 수행하는 관계입니다. 역관계는 때때로 함수가 아닐 수 있으므로 주의해야합니다. 함수가 전단사함수이면 역관계도 함수가 되고 이런 역관계를 역함수라고 합니다. 이렇게 역함수가 존재하는 함수를 가역적이라고 합니다.

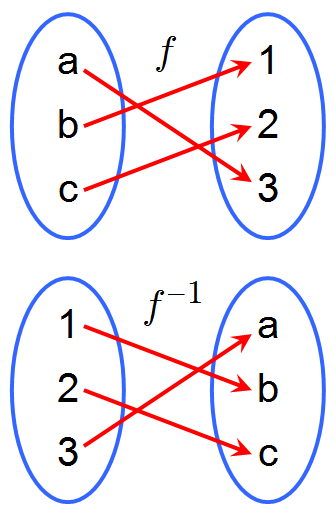
https://en.wikipedia.org/wiki/Inverse_function

📄합성함수

함수 f와 g가 있을 때, f의 출력값이 함수 g의 입력값이 되는 방법으로 결합된 함수를 두 함수의 합성이라고 합니다. 여기서 함수 f의 출력값을 함수 g가 입력값으로 받아들일 수 있어야 합니다. 즉, f의 치역은 g의 정의역에 포함되어야 한다는 의미입니다.

\[\forall x \in X, (g \circ f)(x) \equiv g(f(x))\]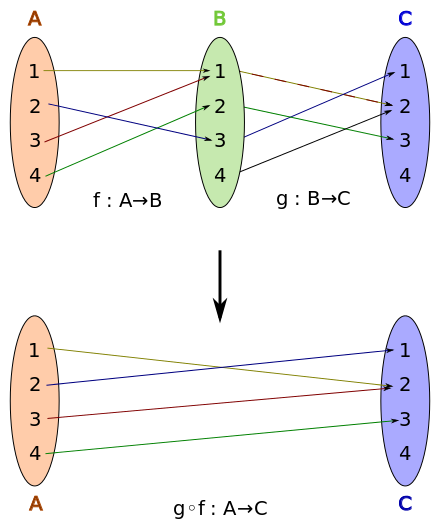

https://en.wikipedia.org/wiki/Function_composition

📚함수 종류

📄계승함수

정수 n에 대한 계승함수 n!은 아래와 같이 정의됩니다.

\[n! = \displaystyle \prod_{k=1}^{n} k=1 \times 2 \times 3 \times ... \times n \; (단, 0! = 1)\]

재귀적으로 표현하면 아래와 같습니다.

\[n! = \begin{cases} 1 &\text(n = 0) \\ n \times (n-1)! &\text(n > 0) \end{cases}\]

📄바닥함수와 천장함수

• 바닥함수
  바닥함수는 실수 x에 대해 x보다 작거나 같으면서 가장 큰 정수를 구하는 함수입니다.
  
  \(\lfloor x \rfloor\) 또는 floor(x)로 표기합니다.

• 천장함수
  천장함수는 실수 x에 대해 x보다 크거나 같으면서 가장 작은 정수를 구하는 함수입니다.
  
  \(\lceil x \rceil\) 또는 ceiling(x)로 표기합니다.

📄나머지 함수

나머지 함수는 정수 n과 자연수 m에 대해, n을 m으로 나누었을 때 나머지 r을 구하는 함수입니다. n mod m으로 표기합니다. 나머지 함수를 모듈러 함수 또는 mod 함수라고도 부릅니다.

정수 n, m이 있을 때, n을 m으로 나눈 몫을 \(\lfloor \frac{n}{m} \rfloor\) 이라고 하면 나머지는 n mod m입니다. 따라서 아래와 같은 식을 표현할 수 있습니다.

\[n = m \lfloor \frac{n}{m} \rfloor + n \; mod \; m\]

위 식을 n mod m에 대한 식으로 변환하면 아래와 같습니다.

\[n \; mod \; m = n - m \lfloor \frac{n}{m} \rfloor\]

📄해시함수

해시기법은 자료를 입력할 때부터 검색하기 쉬운 위치에 삽입하는 방법으로 입력할 자료로부터 자료가 저장될 위체를 결정하는 해시함수가 핵심입니다.

• 나눗셈 이용
  해시함수는 정수의 큰 집합에서 작은 집합으로 정의된 함수로서, 보통 나머지 함수를 사용하여 큰 집합을 작은 집합으로 사상(매핑)합니다.
  
  8자리 학번 n이 있다고 했을 때, 10개 원소를 갖는 작은 집합 {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}로 대응하는 함수는 아래와 같습니다.
  
  \(h(n) = n \; mod \; m\)
  
  학번이 20230501이라고 할 때 해시함수를 통한 출력값은 아래와 같습니다.
  h(20230501) = 20230501 mod 10 = 1

• 곱셈 이용
  해시함수는 곱셈을 이용하기도 합니다. 큰 입력값을 0과 1 사이의 값으로 대응시킨 다음 해시 테이블의 크기를 곱하여 0과 m-1 사이의 정수값으로 팽창시킵니다. x를 입력값, m을 해시 테이블의 크기, α를 0과 1 사이의 상수라고 할 때 해시함수 \(h(x) = \lfloor m(\alpha x \; mod \; 1) \rfloor\)을 사용할 수 있습니다.

  • 처리순서
    1. 임의의 입력값 x에 0과 1 사이의 값 α를 곱하여 소수 부분만 취합니다.
    2. 얻은 소수 부분에 m을 곱하여 정수 부분을 취합니다.(바닥함수, 천장함수 사용)
    3. 결과값 h(x)에 해당하는 저장공간을 할당합니다.