[DiscreteMath]관계

📚기본사항

📄관계

두 집합 X와 Y에 대하여 곱집합 X × Y의 부분집합 R을 X에서 Y로의 관계라고 말합니다. x와 y가 각각 X와 Y의 원소이고 \((x, y) \in R\)이면 \(xRy\)로 표기하고, x는 y와 R의 관계가 있다라고 합니다. \((x, y) \notin R\)이면 \(x\overline{R}y\)로 표기하고, x는 y와 R의 관계가 없다라고 합니다. X, Y 두 집합이 X = Y를 만족하면 이들 사이의 관계 R을 X에서의 관계라고 합니다.

📚관계의 표현

📄화살표 도표

관계를 화살표 도표로 나타내는 방법은 예제를 통해 알아보겠습니다.
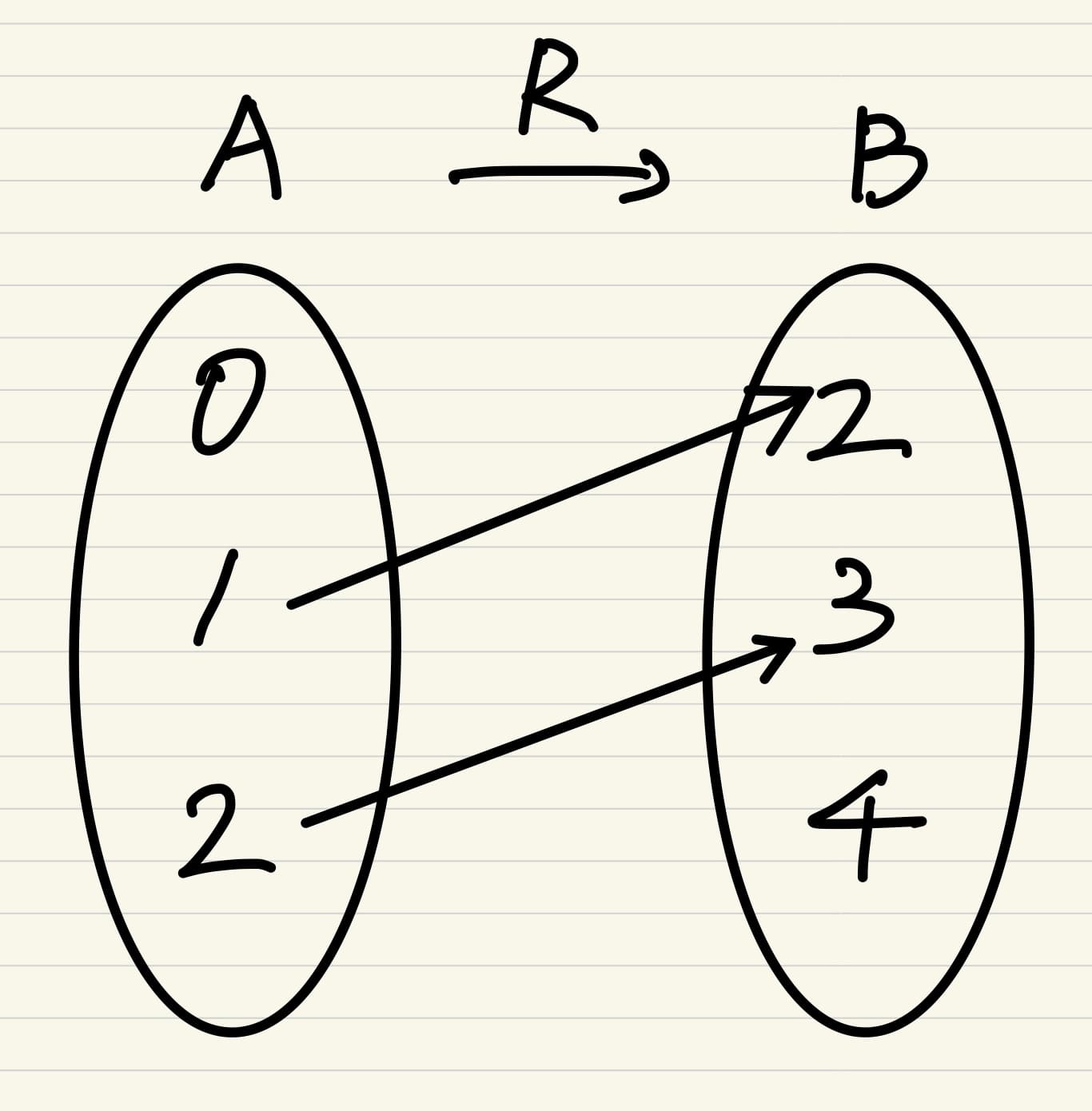
집합 A = {0, 1, 2}, 집합 B = {2, 3, 4}이 있을 때, A에서 B로의 관계 R은 \(R = \{(a, b)| b = a + 1,\;a \in A, b \in B \}\)로 정의된다고 해보겠습니다.

관계 R에 대한 화살표 도표를 그리면 아래와 같습니다.

📄부울 행렬

집합 X와 Y가 아래와 같이 있습니다.

\[X = \{x_1,\;x_2,\;...,\;x_m \}, \quad Y = \{y_1,\;y_2,\;...,\;y_n \}\]

X에서 Y로의 관계 R은 다음과 같이 m × n 크기의 부울행렬 M_R로 나타낼 수 있습니다.

\[M_R = \begin{pmatrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ ... & ... & & ... \\ a_{m1} & a_{m2} & ... & a_{mn} \\ \end{pmatrix} , \quad a_{ij} = \begin{cases} 1 : (x_i,y_j) \in R \\ 0 : (x_i,y_j) \notin R \end{cases}\]

위에서 화살표 도표로 나타냈던 R을 부울행렬로 나타내면 아래와 같습니다.

\[M_R = \begin{pmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{pmatrix}\]

📄방향 그래프

두 점을 서로 연결하는 선으로 이루어진 도형을 그래프라고 하는데 그래프는 나중에 더 자세하게 다루겠습니다.

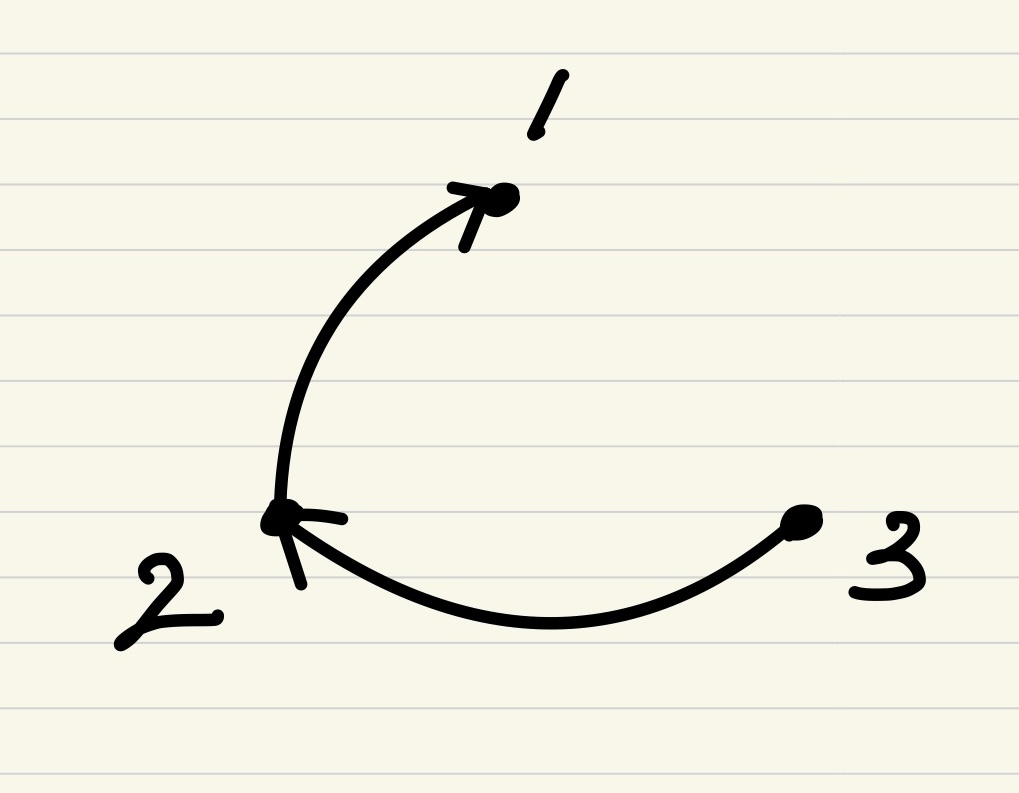
위에서 부울행렬로 표현했던 R을 방향그래프로 나타내면 아래와 같습니다.

📚관계의 성질

📄반사적(reflexive)

집합 A에서의 관계 R이 반사적이 되려면 A의 모든 원소가 자기 자신과 관계를 가져야합니다.

\[모든 a \in A에 대해 (a, a) \in R\]

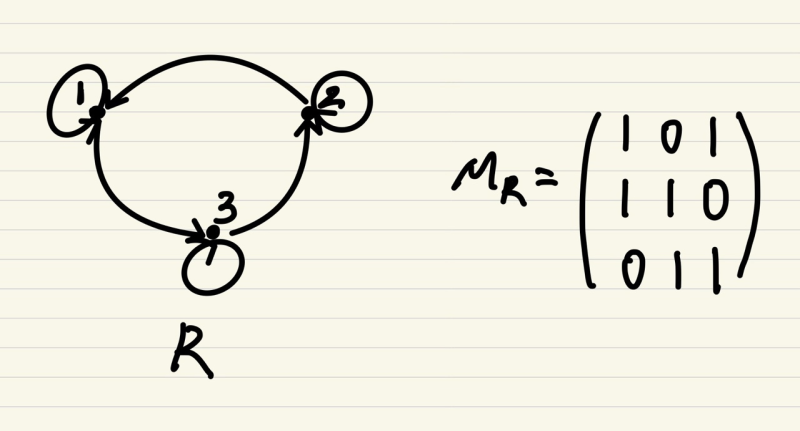
관계가 반사적일 경우 부울행렬의 대각원소가 모두 1인 것을 확인할 수 있습니다.

📄대칭적(symmetric)

집합 A에서의 관계 R이 대칭적이 되려면 R에 포함된 모든 원소가 대칭되는 관계를 가져야 합니다.

\[모든 a, b \in A에 대해 (a, b) \in R일 때 (b, a) \in R\]

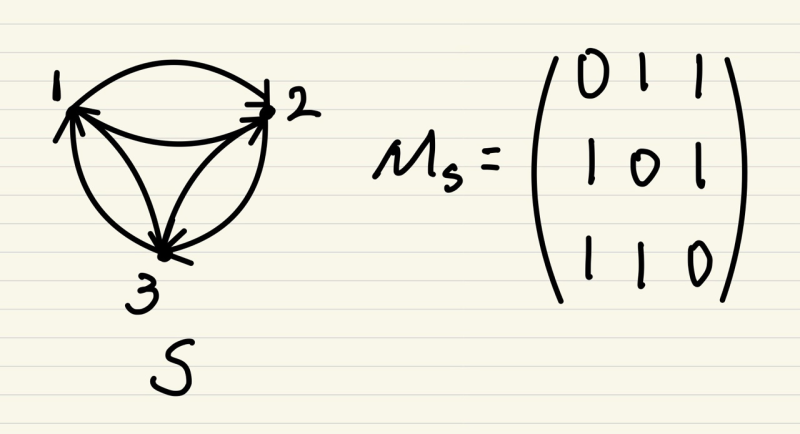
관계가 대칭적일 경우 부울행렬이 대칭행렬이 됩니다.

📄추이적(transitive)

집합 A에서의 관계 R이 추이적이 되려면 R에 포함된 모든 원소들에 대해 \((a, b) \in R\)이고, \((b, c) \in R\)이면 \((a, c) \in R\)이어야 합니다.

\[모든 a, b, c \in A에 대해 (a, b) \in R이고 (b, c) \in R일 때, (a, c) \in R\]

📚관계의 종류

📄역관계

집합 X에서 집합 Y로의 관계 R이 있을 때, 관계를 구성하는 각 순서쌍의 원소의 순서를 바꾸면 Y에서 X로의 관계가 되고, 이것을 역관계라고 합니다. \(R^{-1}\)로 표기합니다.

\[R^{-1} = \{(y,x)|(x,y) \in R\}\]

📄합성관계

집합 A에서 집합 B로의 관계 R이 있고, 집합 B에서 집합 C로의 관계 S가 있을 때, R을 적용하고 S를 적용하여 A에서 C로의 관계를 만들 수 있는데 이것을 합성관계라고 합니다.

\[S \cdot R = \{(a,c) \in A \times C|a \in A, b \in B, c \in C, (a,b) \in R, (b,c) \in S\}\]

❗️R을 적용하고 S를 적용하는 합성관계 기호가 \(S \cdot R\)로 표기되는 것을 주의합니다.

📄동치관계

집합 A에서의 관계 R이 반사적, 대칭적, 추이적이면 R은 동치관계라고 합니다.

집합 X에서의 관계 R이 있을 때, 임의의 원소 a, b, c에 대해 \((a, a) \in R_{(반사적)}\)을 만족하고, \((a, b) \in R\)이면 \((b, a) \in R_{(대칭적)}\)을 만족하고, \((a, b) \in R\)이고 \((b, c) \in R\)일 때, \((a, c) \in R_{(추이적)}\)를 만족하면 R을 동치관계라고 합니다.

• 나머지 함수
  나머지 함수는 하나의 식의 나머지를 구하는 함수입니다. 간단하게 예를 들면, 5 mod 3 = 2이 됩니다.

• 모듈로 합동
  두 정수 m, n에 대해 양의 정수 d로 나머지 연산을 했을 때, 같은 값이 나오는 경우가 있습니다. 이 경우 m과 n은 d에 관한 모듈로 합동이라고 합니다. 모듈로 합동은 기호로 m ≡ n (mod d)이라고 표기합니다. m ≡ n (mod d)를 만족하는 (m, n)의 순서쌍들의 집합을 관계 R이라 했을 때, 다음을 만족합니다.

  • (반사적) 임의의 a에 대해 a ≡ a (mod d)
  • (대칭적) a ≡ b (mod d)이면, b ≡ a (mod d)
  • (추이적) a ≡ b (mod d)이고, b ≡ c (mod d)이면, a ≡ c (mod d)

모듈로 합동은 반사적, 대칭적, 추이적 성질을 만족하므로 동치관계입니다. 또한 d에 임의의 자연수를 대입하더라도 항상 반사적, 대칭적, 추이적이므로 모듈로 합동은 항상 동치관계입니다.

예를 들어, 6 ≡ 16 (mod 10)은 6 mod 10 = 6, 16 mod 10 = 6이므로 모듈로 합동입니다.

📄동치류

집합 A에서의 관계 R이 동치관계일 때, A의 각 원소 a에 대하여 a의 동치류는 a와 R의 관계를 가지는 A의 원소들의 집합이며, [a]로 표기합니다.

\[[a] = \{x|x \in A,(a,x) \in R\}\]