[LinearAlgebra]직교화 과정과 최소제곱법

📚직교기저

{V, <, >}: 내적공간
\(\tilde{A} = \{A_1, A_2, ..., A_n | < A_i, A_j > = 0, i \neq j\}\)

=> 직교집합
=> 일차독립
=> 직교기저
(\(\tilde{A}\)가 생성하는 V의 부분공간 U의 기저)

어떤 공간에 대해 기저이면서 그 안의 벡터들이 서로 직교하는 것을 직교기저라고 한다.

• 단위직교기저: 직교이면서 단위(자신들의 길이가 모두 1)인 기저

• 직교기저의 장점

{Rⁿ, ·}의 경우
\( \tilde{A} = {E_1, E_2, …, E_n} \)
\( E_i = (0, …, 0, 1, 0, …, 0) \quad \text{(1은 i번째 원소)} \)

\(\tilde{A}\)는 단위직교기저(표준기저)
\( E_i \cdot E_j = 0, E_i \cdot E_i = 1 \quad (i \neq j) \)

📍예

\[\{ R^3, \cdot \}, (a, b, c) = aE_1 + bE_2 + cE_3\]

R³ 공간에서 임의의 벡터가 위의 예처럼 표시될텐데 E₁, E₂, E₃ 앞에 일차결합식에 필요한 계수로 넣어 줄 수 있다는 것이 장점이다.

📄벡터의 일차결합 표현

{V, <, >}: 내적공간
\(\tilde{A} = \{A_1, A_2, ..., A_n\}\) 직교집합
U: \(\tilde{A}\)가 생성하는 부분공간

U에 속한 임의의 벡터 B를 아래와 같이 표시할 수 있다.

\[\begin{align} \forall B &\in U, \\ B &= \frac{<B, A_1>}{<A_1, A_1>}A_1 + \frac{<B, A_2>}{<A_2, A_2>}A_2 + ... + \frac{<B, A_n>}{<A_n, A_n>}A_n \end{align}\] \[B = <B, A_1>A_1 + <B, A_2>A_2 + ... + <B, A_n>A_n\]

(\(\tilde{A}\)가 단위직교기저일 때 즉, < A_i, A_i > = 1)

📄푸리에 계수

\[\vec{OH} = |B| cos\theta \frac{A_i}{A_i}\] \[\frac{<B, A_i>}{<A_i, A_i>}A_i = \frac{|B| |A_i| cos \theta}{|A_i|^2}A_i = \vec{OH}\]

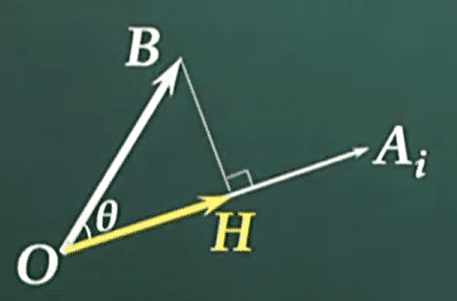
\(\frac{<B, A_i>}{<A_i, A_i>}A_i\)는 정사영벡터를 구하는 것과 같다.

• 푸리에 계수

\[\frac{<B, A_i>}{<A_i, A_i>}\]

B의 A_i방향성분(\(Comp_{A_i}B\))

A_i에 대한 B의 푸리에 계수

📍예제 B를 직교기저의 일차결합으로 표시하면?

B = (1, 2, 3)를 A₁ = (1, 1, 1), A₂ = (1, -2, 1), A₃ = (1, 0, -1)의 일차결합으로 나타내면?

\(A_i \cdot A_j = 0 (i \neq j)\) -> 서로 다른 벡터를 내적하면 0 -> 직교

\(\tilde{A} = \{A_1, A_2, A_3\}\) 직교기저이다.

B의 A_i 방향성분

\[\begin{gather} Comp_{A_1}B = \frac{B \cdot A_1}{A_1 \cdot A_1}A_1 = \frac{1+2+3}{1+1+1}A_1 = 2A_1 \\ Comp_{A_2}B = \frac{B \cdot A_2}{A_2 \cdot A_2}A_2 = \frac{1-4+3}{1+4+1}A_2 = 0A_2 \\ Comp_{A_3}B = \frac{B \cdot A_3}{A_3 \cdot A_3}A_3 = \frac{1+0-3}{1+0+1}A_3 = -1A_3 \end{gather}\] \[B = 2A_1 + 0A_2 + (-1)A_3 = (2, 0, -1)_{\tilde{A}}\]

📚그램-슈미트 직교화

A₁과 A₂ 벡터가 직교하지 않을 때 이 두 벡터를 이용해 직교인 기저 B₁과 B₂를 구하면?

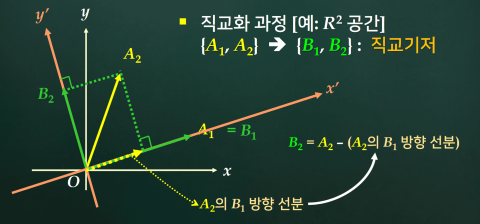
우선 A₁을 B₁과 같다고 둔다.

그 다음 x’축에 수직한 y’축 쪽으로 A₂의 방향성분을 구한다(B₂).

y’축 쪽으로 A₂의 방향성분을 구한다는 의미는 A₂에서 A₂의 B₁ 방향성분을 빼준다는 말이다.(핵심!)

• 그램-슈미트 직교화

{V, <, >}: 내적공간, U < V
\(\tilde{A} = \{A_1, A_2, ..., A_k\}\): U의 기저
=> \(\tilde{B} = \{B_1, B_2, ..., B_k\}\)는 U의 직교기저

\[\begin{align} B_1 &= A_1 \\ B_2 &= A_2 - \frac{<A_2, B_1>}{<B_1, B_1>}B_1 \\ B_3 &= A_3 - \frac{<A_3, B_1>}{<B_1, B_1>}B_1 - \frac{<A_3, B_2>}{<B_2, B_2>}B_2 \\ ... \\ B_k &= A_k - \frac{<A_k, B_1>}{<B_1, B_1>}B_1 - \; ... \; - \frac{<A_k, B_{k-1}>}{<B_{k-1}, B_{k-1}>}B_{k-1} \\ \end{align}\]

📄단위직교기저

내적공간 {V, <, >}의 부분공간 U는 단위직교기저를 갖는다.

U는 직교기저를 갖는다.(그램-슈미트 직교화 과정)
-> 정규화과정을 거치면(벡터를 그 벡터 크기로 나누는 것) -> U는 단위직교기저를 구할 수 있다.

📄직합

내적공간 {V, <, >}의 부분공간 U에 대해

\(U \cap U^\perp = \{O\}, \quad V = U + U^\perp\)이 성립한다.

이때, V는 U와 \(U^\perp\)의 직합(direct sum)으로 이루어졌다고 하고 \(V = U \oplus U^\perp\)로 표시한다.

📍예제 직합

R³의 부분공간 W과 다음과 같을 때 \(R^3 = W \oplus W^\perp\)임을 보여라.

\[W = \{A \in R^3 | A \cdot B = 0, B = (0, 0, 1)\}\]

부분공간 W를 보면 A는 R³의 원소로서 B와 내적이 0이다. 즉, A와 B는 직교이다.

여기서 B는 z축의 단위길이벡터이다. z축에 직교인 것들은 x, y 평면이 될 것이다. 따라서 W는 x, y 평면 전체이다. z축(B)은 W의 직교보공간(\(W^\perp\))이다.

\[\tilde{A} = \{C_1, C_2\} \quad W의 단위직교기저\]

W의 단위직교기저 C₁, C₂가 있다고 했을 때, A는 \(A = aC_1 + bC_2\)와 같이 일차결합식으로 표현할 수 있다.

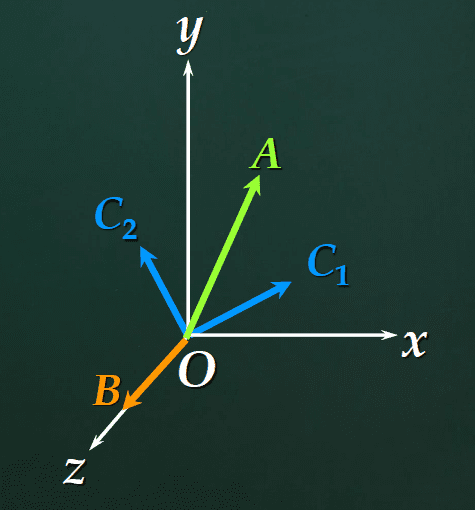
R³ 공간에 임의의 벡터 D가 있다고 했을 때, D는 x, y 평면(W)에 있는 것도 아니고 z축(B)에 있는 것도 아니라고 하면 D는 아래와 같이 표현할 수 있다.

\[\begin{align} \forall D \in R^3 \Rightarrow D &= aC_1 + bC_2 + cB \\ &= (aC_1 + bC_2) + cB \\ &\in W \oplus W^\perp \end{align}\]

📚정사영벡터

(벡터 A의 부분공간 W로의) 정사영벡터

{V, <, >}: 내적공간; W < V, W ≠ {O}
V의 임의의 벡터 A는 다음과 같이 유일하게 표현된다.

\(A = A_W + A^\perp\) (단, \(A_W \in W, A^\perp \in W^\perp\))

만일 B = {B₁, B₂, …, B_k}가 W의 직교기저이면

\[A_W = \frac{<A, B_1>}{<B_1, B_1>}B_1 + \frac{<A, B_2>}{<B_2, B_2>}B_2 + ... + \frac{<A, B_k>}{<B_k, B_k>}B_k\]

• A_W를 A의 W로의 정사영벡터라고 부른다고 약속.

정사영벡터는 근사해를 구하는데 도움이 된다. 어떤 벡터의 가장 가까운 벡터일 수 있다고 이해.

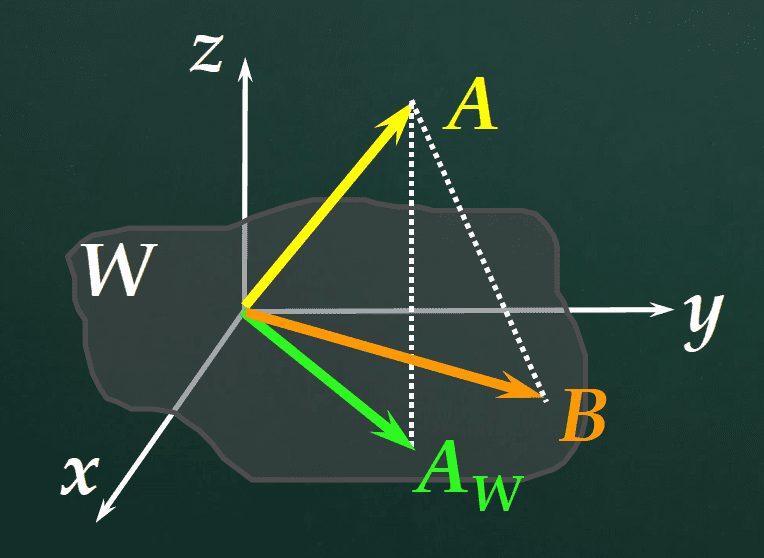
A_W는 W에서 A와 가장 가까운 벡터

\[||A - A_W || \le ||A - B||, (\forall B \in W)\]

📚최소제곱법

• 근사해 구하기

\[\begin{cases} x + y = 2 \\ 2x + y = 2 \\ x - y = 0 \end{cases} \rightarrow \begin{pmatrix} 1 & 1 \\ 2 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix}\]

\(A_1 = (1 \; 2 \; 1)^T, \; A_2 = (1 \; 1 \; -1)^T, \; A = (2 \; 2 \; 0)^T, \; M = (A_1 \; A_2)^T\)이라 하면

위 행렬식을 다음과 같이 나타낼 수 있다.

\[M \begin{pmatrix} x \\ y \end{pmatrix} = A \quad \text{또는} \quad \begin{pmatrix} A_1 & A_2 \\ \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = A\]

{A₁, A₂}로 생성되는 R³의 부분공간을 W라고 하자.

위의 연립 일차 방정식의 근사해를 찾는다는 의미는 A₁, A₂로 생성되는 R³의 부분공간(평면)에서 \(\begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix}\)에 가장 가까운 해를 찾는 것이다.

\[A \neq aA_1 + bA_2 \in W \quad \rightarrow \quad A \notin W \lt R^3\]

W 공간은 A₁과 A₂의 일차결합식으로 나타낼 수 있는데 A는 즉, \((2 \; 2 \; 0)^T\)는 그 부분공간 W(평면)에 존재하지 않기 때문에 A₁과 A₂의 일차결합식으로 나타낼 수 없다는 의미이다. 하지만 A는 R³ 공간에는 포함된다.

• \(A = A_W + A^\perp\)로 표시 가능하다.
• A_W는 W에서 A와 가장 가까운 벡터(정사영벡터)

위의 두 가지 정리를 이용하여 다음과 같은 식을 유도할 수 있다.

\[\begin{pmatrix} A_1 & A_2 \\ \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = A \quad \rightarrow \quad \begin{pmatrix} A_1 & A_2 \\ \end{pmatrix} \begin{pmatrix} a \\ b \end{pmatrix} = A_W\]

A 대신 A와 가장 가까운 벡터 A_W를 이용하여 미지수 a, b를 구하는 문제로 바꿀 수 있다. (A_W는 W의 원소이므로 W 공간상에 한 벡터로서 A와 가장 가까운 벡터이다.)

이때 \((A_1 \; A_2)\)를 M으로 두고 \(\begin{pmatrix} a \\ b \end{pmatrix}\) 를 X로 두면 \(MX = A_W\)와 같이 나타낼 수 있다. 다시 말해, 근사해를 구하는 것은 오른쪽 항을 A 대신 A_W로 뒀을 때, X 값을 구하는 문제로 바뀐다고 말할 수 있다.

📄최소제곱해

M이 m × n 행렬이고 A ∈ R^m일 때, 모든 B ∈ Rⁿ에 대하여

\[||A - M\hat{B} || \le || A - MB ||\]

를 만족하는 \(\hat{B} \in R^n\)를 방정식 MX = A의 최소제곱해라고 약속.

\[\begin{gather} MX = A \Rightarrow A - MX = O \\ \Rightarrow || A - MX || \le || A - M\hat{B} || \le || A - MB || \\ \text{여기서} \hat{B} = A_W \end{gather}\]

📄정규방정식

MX = A에 대한 정규방정식

\[M^TM\hat{B} = M^TA\]

• 최소제곱해와 정규방정식

M = (A₁ A₁ … A₁): m × n 행렬
\(A \in R^m, \hat{B} \in R^n \)

\(\hat{B}\)는 MB = A의 최소자승해
<=> \(\hat{B}\)는 MB = A의 정규방정식(\(M^TM\hat{B} = M^TA\))의 해
(필요충분조건)

📍예제 최소제곱해 구하기

\[\begin{cases} x + y = 2 \\ 2x + y = 2 \\ x - y = 0 \end{cases} \rightarrow \begin{pmatrix} 1 & 1 \\ 2 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix} \rightarrow M\hat{B} = A\]

\(M^TM\hat{B} = M^TA\) 이용하여 \(\hat{B}\)를 구한다.

\[\begin{pmatrix} 1 & 2 & 1 \\ 1 & 1 & -1 \\ \end{pmatrix} \begin{pmatrix} 1 & 1 \\ 2 & 1 \\ 1 & -1 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 & 2 & 1 \\ 1 & 1 & -1 \\ \end{pmatrix} \begin{pmatrix} 2 \\ 2 \\ 0 \end{pmatrix}\] \[\begin{pmatrix} 6 & 2 \\ 2 & 3 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 6 \\ 4 \end{pmatrix} \rightarrow \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 6 & 2 \\ 2 & 3 \end{pmatrix}^{-1} \begin{pmatrix} 6 \\ 4 \end{pmatrix}\] \[\begin{pmatrix} x \\ y \end{pmatrix} = \frac{1}{7} \begin{pmatrix} 5 \\ 6 \end{pmatrix}\]

• 최소제곱해 정리

m × n행렬 M의 위수 = n이면
MB = A의 최소제곱해 \(\hat{B} \in R^n\)는
\( \hat{B} = (M^TM)^{-1}M^TA \)

\( M^TM\hat{B} = M^TA \)
\( M^TM \): (n × m)(m × n) => n차 정방행렬
M의 위수 = n => 영행 아닌 행이 n개(행제형)
=> \( M^TM \)은 영행이 없다. => \( M^TM \)은 정칙행렬
=> \( M^TM\hat{B} = M^TA \) => \( \hat{B} = (M^TM)^{-1}M^TA \)