[LinearAlgebra]선형변환

📚사상

선형변환을 다루기 앞서 사상에 대해 살펴본다.

ƒ ⊂ A ✕ B가 A에서 B로 함수 또는 사상이라고 하는 것은 A의 임의의 원소 a에 대해 B의 원소 b가 유일하게 존재해서 (a, b) ∈ ƒ가 성립한다는 것이다.

순서열 (A, B, ƒ)를 ƒ : A → B로 나타내고 A에서 B로의 사상 ƒ라고 한다. 사상 (A, B, ƒ)에서 A를 정의역, B를 공번역, ƒ를 그래프라고 한다.

• A’ ⊂ A일 때, A’의 ƒ에 의한 상

ƒ(A’) = { f(a) | a ∈ A’ } ⊂ B

• B’ ⊂ B일 때, B’의 ƒ에 의한 원상

ƒ^-1(B’) = { a ∈ A | ƒ(a) ∈ B’ } ⊂ A

A에서 B로의 사상 ƒ(ƒ: A → B)

1. ƒ(A) = B를 만족하면 전사사상이라고 한다.(공역 = 치역)
2. B의 임의의 원소 b에 대해 ƒ^-1(B’)가 공집합 또는 오직 하나의 원소일 때 ƒ를 단사사상이라고 한다.
3. 전사이면서 단사인 경우 전단사사상이라고한다.

사상 T에 대응하는 행렬

T: R² → R³

T(x, y) = (x + y, x - y, 2x + y)를 행렬로 표현이 가능하다.

\[\begin{pmatrix} 1 & 1 \\ 1 & -1 \\ 2 & 1 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ \end{pmatrix} = \begin{pmatrix} x + y \\ x - y \\ 2x + y \\ \end{pmatrix}\]

MA = T(x, y) 형태로 표현이 가능하다.

• 행렬 M을 사상 T에 대응하는 행렬
  
• 사상 T: R^m → Rⁿ를 행렬로 대응시킬 수 있을 때, T를 행렬사상 또는 행렬변환이라고 한다.

📚선형변환

V, W: 벡터공간
T: V → W(사상)
벡터공간 V의 두 벡터 A, B와 실수체의 원소 k에 대해 다음 두 성질을 만족할 때 T를 V에서 W로의 선형변환이라고 한다.

1. T(A + B) = T(A) + T(B)
2. T(kA) = kT(A)

선형변환은 두 연산(벡터끼리의 덧셈연산, 벡터와 실수와의 곱셈연산)을 보존한다.

그리고 선형변환은 일차결합도 보존한다.

위의 두 성질을 합치면 다음과 같다.
T(kA + lB) = T(kA) + T(lB) = kT(A) + lT(B)

벡터 A, B의 일차결합인 kA + lB를 선형변환 T로 보내면 실수 k, l을 보존하고 T(A)와 T(B)의 일차결합으로 변환시킨다.

T: V → W(선형변환)
A, B를 벡터공간 V의 벡터라고 하면 다음이 성립한다.

1. T(O) = O (덧셈의 항등원 보존)
2. T(-A) = -T(A) (덧셈에 대한 역원 보존)
3. T(A - B) = T(A) - T(B) (뺄셈도 보존)

📄선형변환 행렬 표현

Rⁿ 벡터공간에서 정의된 선형변환이 주어졌을 때 이에 대응하는 행렬을 구한다.

T: R^m → Rⁿ(선형변환)

T에 대응되는 행렬 M(n × m행렬)

\[M = (T(E_1) T(E_2) ... T(E_m))\]

E₁, E₂, …, E_m은 기본벡터이고 T(E_i)는 열벡터로 쓴다.

📍예제

T: R³ → R²(선형변환)

T가 T(E₁) = (2, 1), T(E₂) = (-2, 5), T(E₃) = (7, 3)으로 주어질 때 T에 대응하는 행렬과 선형변환 T를 구하라.

R³의 임의의 벡터를 A = (x, y, z)라고 하면 아래와 같이 나타낼 수 있다.

\[T(A) = T(x, y, z) = \begin{pmatrix} 2 & -2 & 7 \\ 1 & 5 & 3 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix}\]

따라서 T에 대응하는 행렬은 \(\begin{pmatrix} 2 & -2 & 7 \\ 1 & 5 & 3 \\ \end{pmatrix}\) 이고,

선형변환은 T(x, y, z) = (2x -2y + 7z, x + 5y + 3z) 이다.

📄선형변환의 합성

S: U → V, T: V → W(선형변환)
U의 임의의 벡터 A에 대해
T ∘ S(A) = T(S(A))로 정의한다.

그러면 T ∘ S: U → W는 선형변환이다. (T ∘ S는 U에서 W로의 선형변환)

위의 정리에서 S에 대응하는 행렬을 M,
T에 대응하는 행렬을 N이라고 할 때,
T ∘ S에 대응하는 행렬은 NM이다.

📚선형변환 성질

📄기본성질

T: V → W(선형변환)

\[\begin{gather} T(k_1A_1 + k_2A_2 + ... + k_nA_n) \\ = k_1T(A_1) + k_2T(A_2) + ... + k_nT(A_n) \\ \\ \\ T(\sum{k_iA_i}) = \sum{k_i}T(A_i) \end{gather}\]

📄기저의 상으로 선형변환 결정

T: V → W

\[\begin{gather} \tilde{A} = \{A_1, A_2, ..., A_n\} = \text{V의 기저 (dimV = n)} \\ \forall B_i \in W(i = 1, 2, ..., n) \\ T(A_i) = B_i \text{만족하는 선형변환 유일하게 존재} \end{gather}\]

📄부분공간

T: V → W
V’ < V → T(V’) < W

T가 벡터공간 V에서 벡터공간 W로의 선형변환일 때 V’를 V의 부분공간이라고 하면 T(V’)는 W의 부분공간이다.

T(V) < W

T(V)는 W의 부분공간이 된다. T(V)를 T에 의한 V의 상이라고 하고 Im(T)로 표기한다. (W 안에 있는 치역)

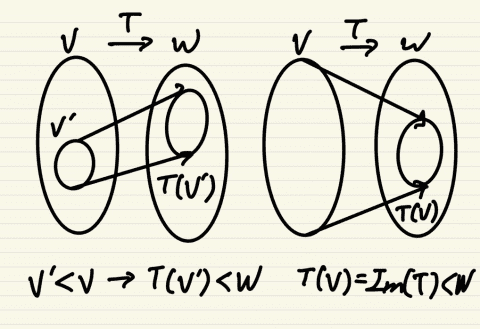
📄일차독립성의 보존

T: V → W (선형변환) ∀ A₁, A₂, …, A_n ∈ V에 대해 모든 T(A_i) (i = 1, 2, …, n)가 W에서 일차독립이면 A_i(i = 1, 2, …, n)도 V에서 일차독립이다.

W의 성질이 V에도 만족한다라고 이해.(역방향)

📄선형변환 전체의 집합

S, T: V -> W (선형변환) ∀ A ∈ V, ∀ k ∈ R에 대해 S + T와 kT 정의.(약속)

(S + T)(A) = S(A) + T(A)
(kT)(A) = kT(A)

선형변환들의 집합이 위의 성질들을 만족한다고 약속한 이유?
-> 사상 S + T와 kT는 V에서 W로의 선형변환이 된다는 것을 증명하기 위해 약속함.

위의 성질들을 약속하고 선형변환이 된다는 것을 찾아서 증명한 이유?
-> 선형변환들의 집합이 벡터공간이라는 것을 보이기 위함.

L(V, W): V에서 W로의 선형변환 전체의 집합
즉, L(V, W) = {T | T : V -> W는 선형변환}

-> L(V, W)는 벡터공간이다.
-> 선형변환을 벡터라고 볼 수 있다.

📚선형변환의 상과 핵

📄부분공간의 보존

T ∈ L(V, W)
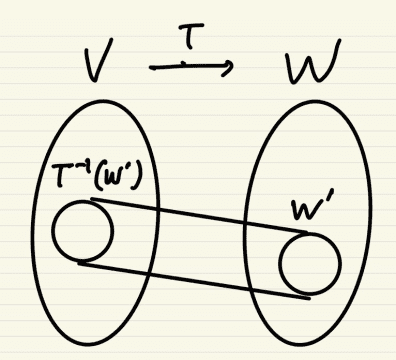
W’ < W -> T^-1(W’) < V

T는 V에서 W로의 선형변환의 원소이다. 따라서 T는 선형변환.

위에서 다뤘던 부분공간에 대한 것과 반대된다고 이해.

W의 부분공간 W’의 역상이 V의 부분공간이 된다라고 이해.

📄선형변환의 핵(커널)

{O} < W -> {O}의 원상 T^-1(O) : Ker(T)로 표현

W에 덧셈에 대한 항등원 영벡터가 있을 때, 원점은 원점으로 보존이 되기 때문에 W의 영벡터에 대한 역상도 V에서 보존된다.(V의 영벡터)

하지만 W의 영벡터에 대한 역상이 하나만 있을 수도 있지만(단사함수) 여러 개 존재할 수 있다.

W의 영벡터에 대한 원상이 집합을 구성한다고 하면 이 집합은 V의 부분공간일 것이다.

이때 만들어진 집합을 Ker(T)라고 부르기로 약속.

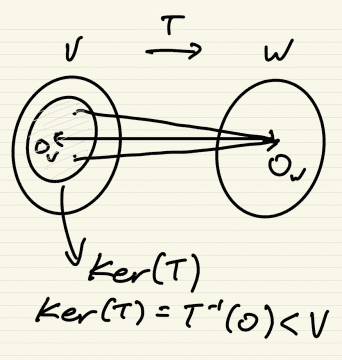
{O} < W -> T^-1(O) = Ker(T) < V
T^-1(O) ≠ Ø(T(O) = O)
if Ker(T) = {O}, then T is injective(단사 함수)

커널이 하나만 있을 때 -> T는 단사함수

• 따름정리

(1) 기저의 보존
T가 단사, \(\tilde{A} = \{A_1, ..., A_n\}\)가 V의 기저
=> \(\tilde{B} = \{T(A_1), ..., T(A_n)\}\)가 T(V)의 기저

(2) 전사와 단사
dim V = dim W => (T가 전사 <=> T단사)

📍예제

T ∈ L(R², R³), T(x,y) = (0,0,x+y), Ker(T) = ?

\[\begin{align} Ker(T) &= \{A \in R^2 | T(A) = O \} \\ &= \{(x,y) \in R^2 | T(x,y) = (0,0,x+y) = (0,0,0) \} \\ &= \{(x,y) | x+y = 0 \} \\ &= \{(x,-x) | x \in R \} \\ &= \{x(1,-1) | x \in R \} \end{align}\]

(x, -x)를 x가 스칼라로서 붙어있는 형태로 변형할 수 있고 (1, -1)은 커널이라는 부분공간의 기저벡터가 될 수 있다. -> (1, -1)을 span해서 사용 가능.

Ker(T)를 구성하는 벡터는 (1, -1) 하나이다. 따라서 커널의 차원(dimension)은 1이 된다.

📄일차독립성의 보존

T ∈ L(V, W), Ker(T) = {O}일 때, A₁, A₂, …, A_n(∈ V)이 V에서 일차독립이면 -> T(A_i) (i = 1, 2, …, n)가 W에서 일차독립이다.(순방향)

📄차원공식

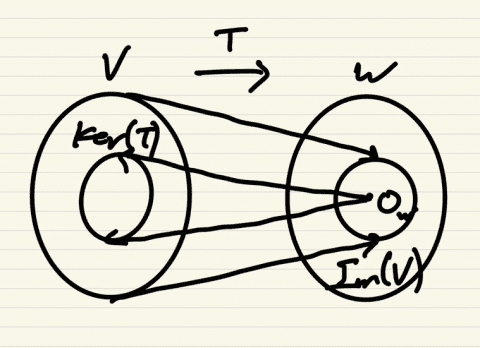
T ∈ L(V, W)일 때, dim V = dim Im(T) + dim Ker(T)

T가 V의 차원을 W로 보존시켜준다고 생각했을 때, V의 차원과 V의 상 Im(V)의 차원이 같지 않을까 생각해 볼 수 있다.(dim V = dim Im(T)) V의 차원을 구할 때 여기서 끝나는 것이 아니라 커널에 대해서도 생각해 볼 수 있다.

위에서 알아보았듯이, W의 영벡터의 원상들이 하나만 있을 수도 있지만 여러 개가 존재해 집합을 이룰 수 있다고 했고 이러한 집합을 Ker(T)이라고 부르기로 했다.

W의 영벡터의 원상이 V의 영벡터로 하나가 아닐 때(T가 단사함수가 아닐 때) 커널이 차원을 만들만한 부분공간이 될 수도 있다. 즉, V에서 W로 가는 커널의 상은 W의 영벡터로 몰려서 차원이 0이 되지만 V의 부분공간인 커널은 차원이 존재하거나 커질 수 있다.

따라서 V의 차원을 구할 때 V의 상 Im(V)의 차원과 Ker(T)의 차원을 더해준다.

• 따름 정리

• T ∈ L(V, W)일 때, dim V = dim W, Ker(T) = {O}
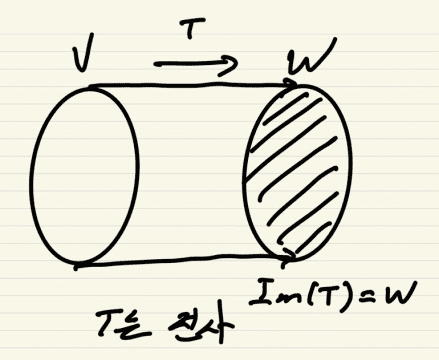
  ->T는 전사(T(V) = Im(T) = W)

Ker(T)가 영벡터만 가질 경우, V의 차원과 W의 차원이 같다면 T에 의한 V의 상 Im(T)이 공역 전체가 된다.

• T ∈ L(R^m, Rⁿ), M = (T(E₁) T(E₂) … T(E_m))
  -> dim T(R^m) = dim Im(T) = rank(M)

행렬 M에 기본행연산을 여러 번해서 행제형 행렬로 만들면 0행이 아래로 깔리는데 이때 0행이 아닌 행의 개수(위수, rank)가 T(R^m)의 차원이다.

dim R^m = dim Ker(T) + dim Im(T) -> m = dim Ker(T) + rank(M)
dim Ker(T) = m - rank(M)

📍예제

T ∈ L(R², R³), T(x, y) = (x + y, x - y, 2x)
dim Im(T) = ?, dim Ker(T) = ?

(1) M(T)

\[M(T) = (T(E_1) T(E_2)) = \begin{pmatrix} 1 & 1 \\ 1 & -1 \\ 2 & 0 \end{pmatrix}\]

(2) dim Im(T) = rank(M)

\[\begin{pmatrix} 1 & 1 \\ 1 & -1 \\ 2 & 0 \end{pmatrix} \to \begin{pmatrix} 1 & 1 \\ 0 & -2 \\ 0 & -2 \end{pmatrix} \to \begin{pmatrix} 1 & 1 \\ 0 & 1 \\ 0 & 0 \end{pmatrix} \quad rank(M) = 2\]

(3) dim Ker(T) = dim R² - rank(M)

\[2 - 2 = 0\]

📄동형변환, 동형공간

T ∈ L(V, W)이 전단사일 때,
T를 동형변환
V와 W를 동형, V ≈ W로 표기

• 동형변환 성질 T ∈ L(V, W)가 동형변환
  (1) Ker(T) = {O}, Im(T) = W
  (2) dim V = dim W