[LinearAlgebra]선형변환과 행렬

📚좌표계

벡터 A는 2차원 평면 좌표계(직교좌표계)에서 단위 길이 1로 했을 때 x로 한 칸, y로 두 칸 갔기 때문에 아래와 같이 (1, 2)로 표현할 수 있다.

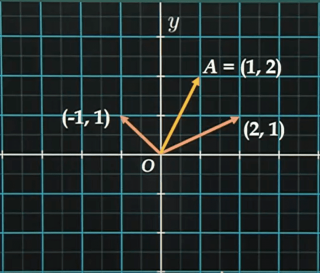
벡터 A 뿐만 아니라 (2, 1)과 (-1, 1) 벡터가 있다고 생각해보자. 이때 (2, 1)을 늘려서(span) 직선을 하나 만들고, (-1, 1)을 늘려서 직선을 만들면 아래와 같이 표현할 수 있다.

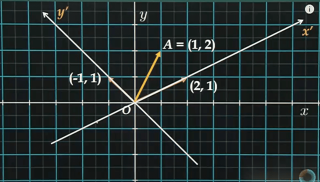
벡터 (2, 1)을 k(상수)배 하면 위 그림의 (2, 1)을 지나는 직선 상의 어떤 점도 표현할 수 있다. 이는 벡터 (-1, 1)에도 동일하게 적용되는 것을 알 수 있다.

위 그림의 (2, 1)을 지나는 직선을 x’축으로 정하고 (-1, 1)을 지나는 직선을 y’축이라고 정하면 새로운 좌표계가 생기는 것을 볼 수 있다. 다만, 이 새로운 좌표계는 직각이 아니다.

여기서 벡터 A는 기존 x축과 y축으로 구성된 직교좌표계에서는 (1, 2)로 표현되지만 새롭게 만들어진 x’축과 y’축으로 이루어진 좌표계에서는 어떻게 표현되는지 알아본다.

A 좌표는 표준 기저에 따른 좌표인데 이것을 (2, 1)이라는 하나의 벡터와 (-1, 1)이라는 하나의 벡터의 일차 결합식으로 나타낼 수 있다. 이 식을 풀면 아래와 같다.

\[\begin{gather} A = (1, 2) = c_1(2, 1) + c_2(-1, 1) \\ \\ 2c_1 - c_2 = 1 \\ c_1 + c_2 = 2 \\ c_1 = 1 \\ c_2 = 1 \end{gather}\]

위 일차연립방정식에서 c₁과 c2₂를 미지수로 놓고 행렬방정식으로 나타내면 아래와 같다.

\[\begin{pmatrix} 2 & -1 \\ 1 & 1 \end{pmatrix} \begin{pmatrix} c_1 \\ c_2 \end{pmatrix} = \begin{pmatrix} 1 \\ 2 \end{pmatrix}\]

식을 풀어서 나온 c₁, c2₂가 새로운 좌표계에서 표현되는 새로운 좌표이다. 즉, A의 좌표 (1, 2)를 기존 직교좌표계가 아닌 x’축과 y’축으로 이루어진 좌표계에서 새롭게 표현하면 (1, 1)이 되는 것이다.

같은 벡터가 좌표계 마다 다르게 표현되면 이를 사용할 때 혼동되기 때문에 새롭게 표현된 좌표는 직교좌표계에서의 좌표와 구분되게 사용한다.

예를 들어, 벡터(2, 1)을 B₁이라고 하고, 벡터 (-1, 1)을 B₂라고 할 때 새로운 기저 \(\tilde{B} = \{B_1, B_2\}\)가 만들어진다. 따라서 새로운 좌표 (1, 1)는 표준 기저가 아닌 좌표이므로 \((1, 1)_{\tilde{B}}\)로 나타낸다. 쉽게 말해, A의 좌표 (1, 2)를 기저 \(\tilde{B}\)를 이용하여 나타내면 (1, 1)이 된다라는 의미이다.

📄일반벡터의 좌표

V: 벡터공간
\(\tilde{A} = \{A_1, A_2, ..., A_n\}\): V의 기저
∀ C ∈ V, C = Σk_iA_i

유클리디안 공간을 포함한 일반벡터공간에는 반드시 기저가 있다. 벡터공간의 어떤 것이라도 기저가 되기 위한 서로 일차독립인 벡터들의 일차결합식으로 나타낼 수 있다. C가 벡터공간 V에서의 임의의 벡터라고 했을 때, C는 k₁A₁, k₂A₂, …, k_nA_n으로 표현할 수 있다. 여기서 k_i들을 순서대로 적으면 아래와 같다.

C ≡ (k₁, k₂, …, k_n)_{\(\tilde{A}\)}

기저 \(\tilde{A}\)로 표현한 벡터 C의 좌표 -> k₁, k₂, …, k_n (기저의 순서가 바뀌면 좌표도 바뀐다! -> 순서기저)

📍예제(벡터의 기저를 바꿔서 표현)

R³ 공간 벡터의 좌표

\(\tilde{A} = \{A_1=(1, 0, -1), A_2=(0, 1, -1), A_3=(0, 0, 1)\}:R^3\)의 기저 \(\tilde{A}\)로 표현한 C = (1, 3, -4)의 좌표는?

\[\begin{align} C = (1, 3, -4) &= k_1(1, 0, -1) + k_2(0, 1, -1) + k_3(0, 0, 1) \\ &k_1 = 1 \\ &k_2 = 3 \\ &-k_1 - k_2 + k_3 = -4 \\ \\ &= 1(1, 0, -1) + 3(0, 1, -1) + 0(0, -1, 1) \\ \\ &C = (1, 3, 0)_{\tilde{A}} \end{align}\]

📚선형변환의 행렬 표현

📄사상의 행렬

V, W: 벡터공간
T: V -> W(사상)

\(\tilde{A} = \{A_1, A_2, ..., A_n\}\)은 V의 기저

\(\tilde{B} = \{B_1, B_2, ..., B_n\}\)은 W의 기저

이때 사상 T에 의한 \(\tilde{A}\)의 상을 기저 \(\tilde{B}\)로 표현한 행렬을
\((T)^{\tilde{A}}_{\tilde{B}} = (T(A_1)_{\tilde{B}} \quad T(A_2)_{\tilde{B}} \quad T(A_n)_{\tilde{B}} )\) 으로 정의한다.

V의 원소에 벡터 A₁, A₂, …, A_n 이 있을때, 이 원소들의 T에 의한 \(\tilde{A}\)의 상은 T(A₁), T(A₂), …, T(A_n) 이다. 이것들을 기저 \(\tilde{B}\)로 표현하면 새로운 좌표가 구해지는데 이 좌표들을 열벡터로 나타낸다는 의미이다.

아래 표현은 동치이다.

사상 T: V -> W가 선형변환 <–> T에 대응되는 행렬(T에 의한 \(\tilde{A}\)의 상을 기저 \(\tilde{B}\)로 표현한 행렬)이 \((T)^{\tilde{A}}_{\tilde{B}}\)으로 표시되는 것.

dim V = n, dim W = m
->L(V, W) ≈ M_mn(R)

위 정리의 의미는 다음과 같다.

• 선형변환의 벡터공간과 행렬의 벡터공간은 동형공간이다.(일대일 대응)
• 선형변환 T ∈ L(V,W)의 성질을 알아보는 것은 행렬 M ∈ M_mn(R)의 성질을 알아보는 것과 같다는 의미이다.

선형변환의 성질을 알아보기 어려울 때 일대일 대응되는 행렬을 알아봄으로써 그 성질을 조금 수월하게 찾을 수 있다고 이해.

📍예제

• 선형변환을 행렬로 표현

\[T \in L(R^3,R^2), T(x, y, z) = (x + z, y + z)\]

(1)\(\tilde{S_3}, \tilde{S_2}\): 표준기저
\(\tilde{S_3} = \{E_1, E_2, E_3\}, \quad \tilde{S_2} = \{E_1, E_2\}\)

T에 의한 \(\tilde{S_3}\)의 상을 기저 \(\tilde{S_2}\)로 표현한 행렬을 구하는 방법이다.

\[\begin{gather} T(1, 0, 0) = (1 + 0, 0 + 0) = (1, 0)_{\tilde{S_2}} \\ T(0, 1, 0) = (0 + 0, 1 + 0) = (0, 1)_{\tilde{S_2}} \\ T(0, 0, 1) = (0 + 1, 0 + 1) = (1, 1)_{\tilde{S_2}} \end{gather}\]

이 좌표들을 열벡터로 표현하면 구하고자 하는 행렬을 얻을 수 있다.

\[(T)^{\tilde{S_3}}_{\tilde{S_2}} = \begin{pmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix}\]

• 동일한 선형변환의 행렬 표현

V: 벡터공간, \(\tilde{A} = \{A_1, A_2, A_3\}\)은 V의 기저, \(T \in L(V, V)\)
\(T(A_1) = A_1 + A_3, T(A_2) = A_1 - A_3, T(A_3) = A_1 + A_2 - A_3\) -> T에 의한 \(\tilde{A}\)의 상을 기저 \(\tilde{A}\)로 표현한 행렬은?

\[\begin{align} &T(A_1) = A_1 + A_3 = 1 \times A_1 + 0 \times A_2 + 1 \times A_3 = (1, 0, 1)_{\tilde{A}} \\ &T(A_2) = A_1 - A_3 = 1 \times A_1 + 0 \times A_2 + (-1) \times A_3 = (1, 0, -1)_{\tilde{A}} \\ &T(A_3) = A_1 + A_2 - A_3 = 1 \times A_1 + 1 \times A_2 + (-1) \times A_3 = (1, 1, -1)_{\tilde{A}} \end{align}\]

구해진 좌표들을 열벡터로 해서 행렬을 만들면 된다.

\[(T)^{\tilde{A}}_{\tilde{A}} = \begin{pmatrix} 1 & 1 & 1 \\ 0 & 0 & 1 \\ 1 & -1 & -1 \end{pmatrix}\]

📚기저 변환

기저변환은 행렬의 대각화, 영상압축 등에 활용된다.

선형변환 T의 행렬 표현(기저 변환에 따른 동일한 선형변환 T의 행렬 변화)

\(T \in L(V, V), \tilde{A}, \tilde{B}\)는 V의 기저

\[(T)^{\tilde{A}}_{\tilde{A}} \quad \rightarrow \quad (T)^{\tilde{B}}_{\tilde{B}}\] \[\tilde{A} \quad \rightarrow \quad \tilde{B}\]

기저 \(\tilde{A}\)로 표현한 행렬을 기저 \(\tilde{B}\)로 표현한 행렬로 바꾸면(좌표계를 바꾸면) 둘 사이에 어떤 관계가 있을까 생각해본다.

📄항등변환

I ∈ L(V, V) ∀ A ∈ V, I(A) = A

정의역에 있는 모든 원소에 대해 모두 치역으로 그대로 보내준다는 의미.(변환인데 항등원 처럼 역할을 한다고 이해. 비슷한 예로 단위행렬 -> 행렬인데 곱셈에 대한 항등원)

📄기저변환행렬

\(\tilde{A} = \{A_1, A_2, ..., A_n\}\), \(\tilde{B} = \{B_1, B_2, ..., B_n\}\)은 V의 기저

-> \((I)^{\tilde{A}}_{\tilde{B}}\)

\(\tilde{A}\)에서 \(\tilde{B}\)로의 기저변환행렬. 이것은 항등변환에 대한 행렬이다!

📍예제

\(\tilde{A} = \{A_1, A_2, A_3\}\), \(\tilde{B} = \{A_2, A_1 - A_2, A_2 + A_3\}\)은 V의 기저, I ∈ L(V, V)
-> \(\tilde{A}\)에서 \(\tilde{B}\)로의 기저변환행렬은?

\[\begin{align} &I(A_1) = A_1 = 1 \times A_2 + 1 \times (A_1 - A_2) + 0 \times (A_2 + A_3) = (1, 1, 0)_{\tilde{B}} \\ &I(A_2) = A_2 = 1 \times A_2 + 0 \times (A_1 - A_2) + 0 \times (A_2 + A_3) = (1, 0, 0)_{\tilde{B}} \\ &I(A_3) = A_3 = (-1) \times A_2 + 0 \times (A_1 - A_2) + 1 \times (A_2 + A_3) = (-1, 0, 1)_{\tilde{B}} \end{align}\] \[(I)^{\tilde{A}}_{\tilde{B}} = \begin{pmatrix} 1 & 1 & -1 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \end{pmatrix}\]