[LinearAlgebra]일차연립방정식

September 2, 2023

📚일차연립방정식

가장 간단한 일차 방정식은 다음과 같다.

\[ax = b\]

a는 계수, b는 상수, x는 구하고자 하는 미지수라고 한다. 어떤 수 s가 as = b를 만족할 때 s를 일차방정식의 해라고 한다.

임의의 일차방정식의 해는 계수 a와 상수 b가 어떤 값이냐에 따라 다음과 같이 세 가지 경우로 나뉜다.

a = 0, b = 0
방정식은 \(0x = 0\)이 되어 어떤 값이라도 해가 된다. 이 경우 방정식은 무한 개의 해를 갖는다. 이를 부정인 해라고도 한다.
a = 0, b ≠ 0
방정식은 \(0x = b(b \neq 0)\)가 되어 어떤 x도 해가 될 수 없다. 이 경우 해가 없는 불능인 해를 갖는다.
a ≠ 0
a의 곱셈에 대한 역원 a^-1이 존재하여 방정식의 양변에 곱해 주면 \(a^{-1}ax = a^{-1}b\)이고, 따라서 \(x = a^{-1}b\)가 된다. 역원은 유일하므로 이 경우 방정식은 유일한 해를 갖는다.

일차연립방정식을 푸는 가장 간단한 방법은 소거법을 이용하는 것이다. 소거법이란 연립방정식의 한 방정식에서 하나의 미지수를 없애기 위해 다른 방정식에 적당한 값을 곱한 다음 해당 방정식에 더해주는 방법이다.

소거법은 아래와 같은 세 가지 연산을 이용하여 연립방정식을 변형시킨다. 이는 동일한 해집합을 가지면서도 보다 풀기 쉬운 형태의 연립방정식으로 변환해 나가는 방법이다.

방정식에 관한 세 가지 기본연산
1. 두 방정식을 교환한다
2. 한 방정식에 0이 아닌 상수를 곱한다
3. 한 방정식에 임의의 상수를 곱하여 다른 방정식에 더한다

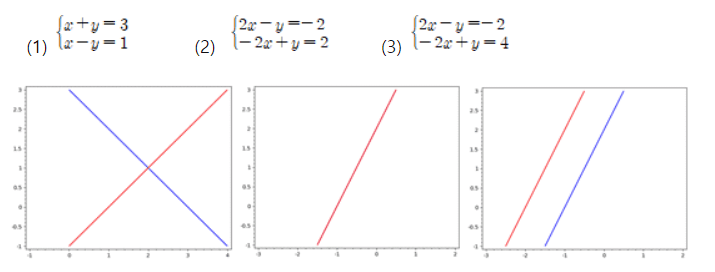
모든 선형연립방정식의 가능한 세 가지 해는 다음과 같다.

SolutionSet